As homeschoolers we are always on the lookout for educational board games for kids. To use Outfoxed as a teaching tool for the process of elimination was my initial thought on what its educational value was. Using it to teach chance (probability) and statistics then came as an afterthought. It turned out to be a very exciting way to teach these concepts in simple terms to my 8 year old granddaughter. We had been doing some roll the dice experiments to investigate chance, and then moved on to playing Yahtzee to gain a deeper understanding how adding in more dice and different outcomes could create more complexity in our experiments. Then I realised that Outfoxed could serve as an even more interesting game to do a little research with due to the additional variables within the game. With Outfoxed, it’s not just dice that have an impact on the game, there are other chance concepts involved in the game.

What Does Chance or Probability in Mathematics Have to do with Outfoxed?

Probability is the concept used to predict the likelihood of an event to occur determining the total number of possible outcomes. In terms of something a younger child could understand, looking at the various possible combinations that could occur from the rolling of the 3 dice is a great learning experience.

Statistics is the analysis of events governed by probability where data is gathered, collated, analysed and presented in a way that helps to represent complicated data in an easy way that is understandable. Graphs, diagrams, tables, etc., are ways to present your findings so that analysis is easier and demonstrating to others is simpler when presenting those findings. Here, in the case of younger children, finding a way to table the various combinations, or just to demonstrate them, can go a long way to learning an important life skill.

Ways to teach the concept of probability include the use of dice, cards, coins, and spinners, to demonstrate the outcomes of random events, and make predictions, calculations and observations based on them. Playing a game such as Outfoxed with more variables is a great way to depict even more possible ways to see the concept of chance in action.

Variables in the game Outfoxed that affected the outcome of the game in terms of a win or a loss include;

• Suspect cards pulled (16 possible suspects)
• Thief card chosen (16 possible thieves)
• 3 dice increasing the number of possible combinations and increasing the chance of the fox getting away
• Rolling the required number of Paws or Eyes on the dice to gain a clue or a suspect.
• Once enough Paws (Clues) are rolled, whether or not you have enough moves on the dice to move to a paw space to call for a clue or will fall short.
• Clue tokens drawn (12 possible options)
• Dice rolls for the movement of the fox
• Shuffling of the cards and tokens
• A total of 3 different suspect clues to match with one thief
• Decisions of players

All of these added a variety of ways players could win or lose the game, making the results of each game played even more random and varied than if it had been played with just dice. Some games were lost and others won. Sometimes we had the same thief for more than one game in the possible 16 thief cards, which was not expected. One in particular, was the thief “Gertrude” which occurred 6 times across 15 games. This was totally unexpected to have such a large number of times it was drawn in so small a number of games. That is almost half of the games played

How Did I Use Outfoxed as a Teaching Tool for Probability & Chance?

I decided it would be a great opportunity to do an experiment on using 3 different strategies to play the game across a set number of games played. In our case, we initially planned to play 30 games, with 10 games operating on Strategy 1, 10 games using Strategy 2 and the last 10 games using Strategy 3 which I will outline shortly. Due to time constraints we had to reduce the number of games by half down to 15 games, 5 of each strategy. My granddaughter would make guesses or think of a hypothesis as to the outcome of a win or lose for each strategy and from our results we would determine if one strategy worked better than another strategy to obtain more wins than losses overall. Chance and Probability would come into play during out discussions of the results, for example, introducing the concept of possible combinations of dice rolls, guessing wins or losses in the game, predicting outcomes, observing chance in action, witnessing unexpected occurrences, using strategy based on our current understanding and then learning how to apply new knowledge to future games.

Just a quick reminder here that the possible combinations for 6 sided dice are:

1 dice = 6

2 dice = 6 x 6 = 36

3 dice = 6x6x6 = 216

Therefore there are 216 possible combinations of the dice rolls in Outfoxed

There are 12 clue cards but you need to obtain 3 correct clues. Apparently there are 220 possible combinations of 3 from a set of 12 objects according to google. They used a specific formula that is too advanced to put into a blog aimed at teaching younger children a basic understanding.

Our 3 Different Strategies

Strategy 1 – Calling For Clues First – was played attempting to get all 3 correct clues from the 12 clue cards first before calling for suspects and determining the thief. To do this, we had to attempt to throw the dice and get all 3 dice showing the clue paw prints and then we could call the clue. Once all 3 correct clues were uncovered, then we could start calling for suspects to match the suspect with the 3 clues and find the thief.

My granddaughter’s hypothesis for Strategy 1 was that we would lose more games than win.

Strategy 2 – Calling For Suspects First – was played by attempting to expose all 16 of the suspect cards before choosing to roll for clues. For this, all 16 cards would need to be uncovered, instead of in strategy 1 where you could move on as soon as the 3 correct clues were found. At the point of all 16 cards being used, then calling for clues would begin.

My granddaughter’s hypothesis for Strategy 2 was that we would win more games than lose.

Strategy 3 – Maintaining 2 suspects uncovered while throwing the dice for clues usually. For this, we throw for clues until a suspect is eliminated, or both if the clues eliminate them at the same time, then throw to draw another suspect card or 2, and continue throwing for clues, and so on, until the thief is discovered.

My granddaughter’s hypothesis for Strategy 3 was that we would win the most games.

We took notes through the games for each strategy for the sake of comparison and observe how chance plays a role in the outcomes of each game:

1. Win or Loss
2. At what number of turns was the first correct clue drawn, then the second, and then the third (this would be different for each game and therefore shows that chance is involved. Some games clues might be uncovered quickly, other games clues might not be uncovered until near the end of the game, and then other games, all 3 correct clues may not be uncovered if the fox escapes first)
3. How many turns it took before we got all 3 correct clues. (Once again, this will be different for each game and may not all be uncovered before the fox escapes)
4. How many turns to eliminate all of the suspects
5. How many spaces (or turns) left before the fox escapes (Varies throughout the game)
6. Who was the thief? (Believe it or not we had a very surprising result with our thief cards. From 16 suspects, we had one thief drawn 6 times across 15 different games, but only technically had a 1 in 16 chance each time of being drawn). Which means that there may have been other factors involved in the drawing of the cards, such as wear and tear on the cards from being placed into the card holder. The same person shuffling the cards in the same way and same number of times may have contributed to the outcome here too.

Table of Notes Taken During 15 Games of 3 Different Strategies

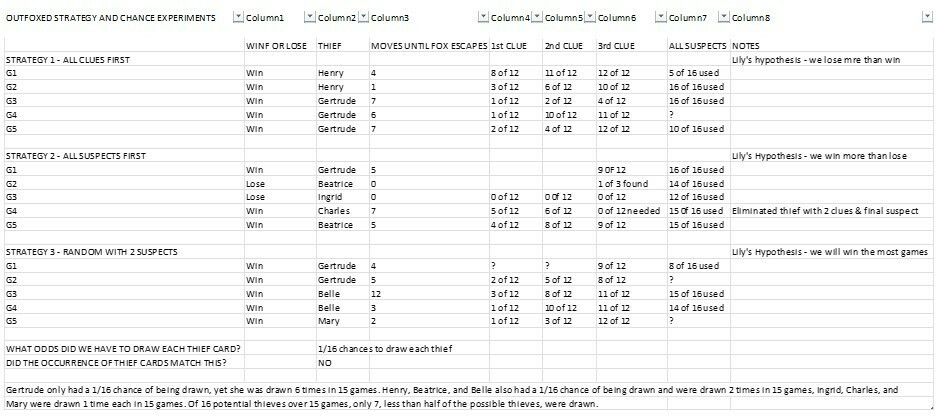
Once we compiled all of the notes and put them into a table (see above), the next step was to discuss our findings and try to reach some kind of conclusion. Was my granddaughter correct in her hypotheses? Was there a strategy that was the obvious winner of the 3? Based on your results, would you expect to get similar results the more games are played, or a significant difference. Would it be an interesting experiment to just use one strategy and play many more games to test your hypothesis against a larger number?

For this game I would suggest using it to give a visual representation and to gain a basic understanding that there is such a thing and that the more variables are present, the varying the outcomes will be. I’m not mathematically minded so I won’t go into the many different combinations that you could get with all of the different variables, which is probably much more complex than you would need to be doing at the young age your child is. Of course if you are interested in learning this, you certainly could go to the extra effort and work it all out. There are a couple of blogs that talk about Outfoxed in terms of chance and probability, one of which offers a way to work out how to increase the odds of winning in your favour in almost every game. However, I wouldn’t recommend this because I feel it would spoil the fun of the game too much, due to changing the randomness of the outcomes and ruining all your hard work.

Want to Know More?

We love Outfoxed so much that I’ve written several articles about the game. You’ll find a review here, an “About Outfoxed” style article here, or you can purchase directly from Amazon here. I hope you have enjoyed this article and have the opportunity to use it in your homeschool or teaching tool kit. I’d love to hear about your own experiences and results so please let me know in the comments.

Warm Wishes

Ange